仰向け で 寝る と 咳 が 出る一次不定方程式で、x,yの係数が互いに素でないとき整数解が . 一次不定方程式で、x,yの係数が互いに素でないとき整数解が存在しないことがあるのは何故なのですか? たとえば14x+2y=1なら2(7x+y)=1左辺は偶数、右辺は奇数となり、これを満たす整数x,yの組. 不定方程式の整数解を求めるときに「互いに素」を利用する . 不定方程式の整数解を求めるときに「互いに素」を利用する理由 3(x+2)−7(y+1)=0とあって,3と7が互いに素だから,なぜx+2は7の倍数になるのかがわかりません。 互いに素,だから何なんだ?って感じです。. 一次不定方程式ax+by=cの整数解 | 高校数学の美しい物語. 解答. (x,y) (x,y) が整数のとき, 2x+4y 2x+ 4y は偶数になる。 よって, 2x+4y=1 2x+ 4y = 1 になることはない。 よって,この不定方程式に 整数解は存在しない。 例題2. 3x+5y=2 3x+ 5y = 2 という不定方程式を満たす整数 (x,y) (x,y) は存在するか? 解答. 実は, m m を整数として, (x,y)= (4+5m,-2-3m) (x,y) = (4+ 5m,−2− 3m) とすると, (x,y) (x,y) は解になる。 実際, 3 (4+5m)+5 (-2-3m)=2 3(4+ 5m)+ 5(−2−3m) = 2. となる。 なお, 上記の解 の見つけ方は記事の後半で説明する。 不定方程式の整数解についての定理. 1次不定方程式で知っておきたい3つの基本知識 | 数学の庭. 互いに素のとき必ず整数解を持つ. a a と b b が互いに素のとき ax + by = c a x + b y = c は必ず整数解を持つ. a a と b b が互いに素であれば「解なし」という答えはあり得ないです。 出題者側目線で考えても、 a a と b b が互いに素であることさえ確認すれば「整数解が存在しない」という出題ミスが起こらないのは有難いことかもしれないですね。 一方, a a と b b が互いに素でないときは, 整数解を持つとは限りません。 例えば、 a, b a, b がどちらも3の倍数なら. a = 3a′, b = 3b′ a = 3 a ′, b = 3 b ′ と書けます。 このとき. 【高校数学A】1次不定方程式ax+by=cの整数解の存在条件 . 対偶「a,,bが互いに素でないならばax+by=1の整数解が存在しない」を示すのもほぼ同じである. 次が同値であることも非常に重要である. ax+by=1を満たす整数x, yが存在する ⇔ すべての整数Nはax+byの形で表せる すべての整数Nがax+byの形で表せるとは, ax+by=Nの整数解が存在することを意味する. 例えば, 13は2x+9yの形で表すことも92x+25yの形で表すこともできる. 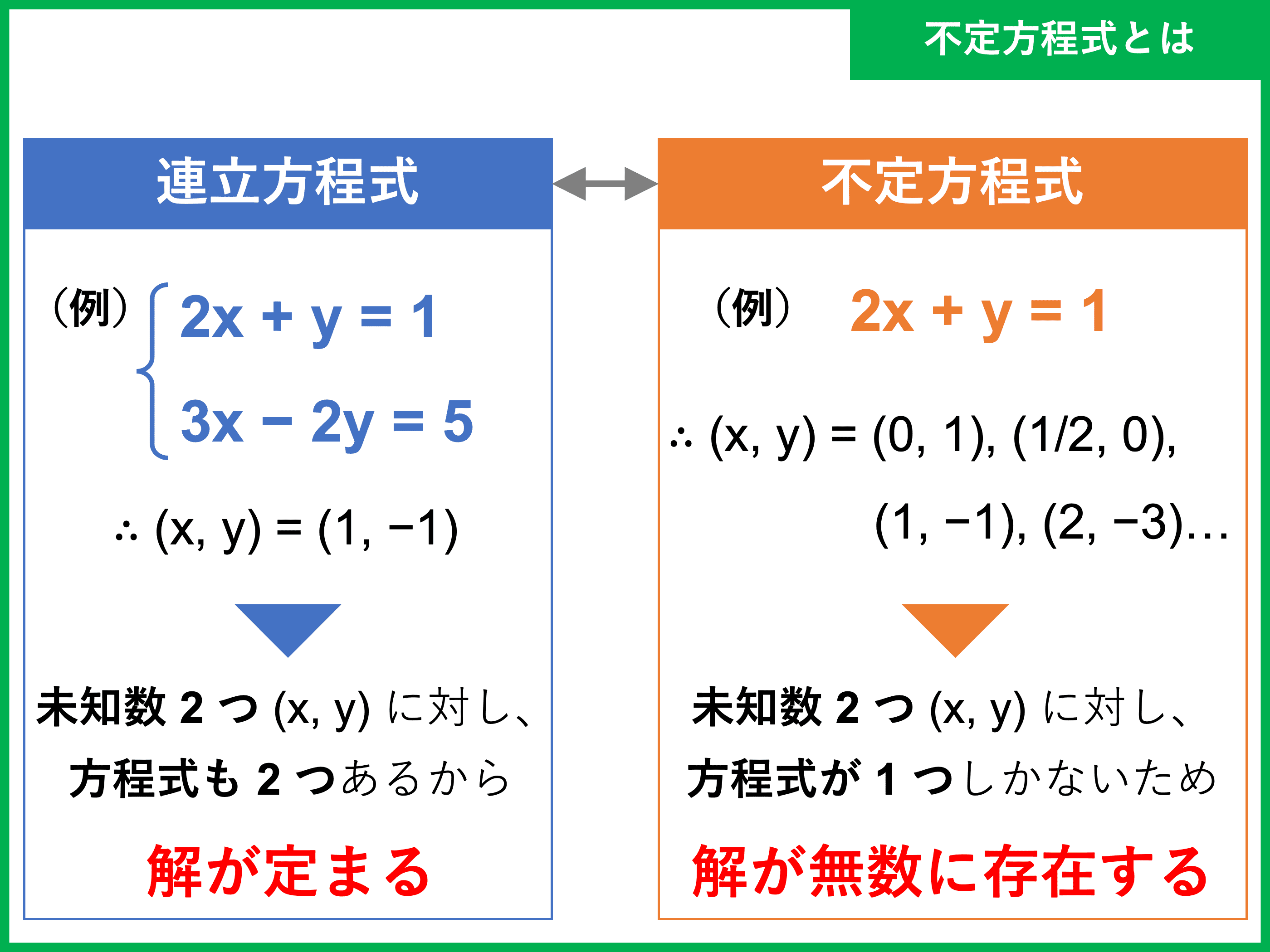
2x+9y=13, 92x+25y=13の整数解が存在することと同じである. 【高校数学の不定方程式】出題パターンに沿って解き方を解説 . また、ユークリッド互除法が使えるのは、不定方程式「ax+by=1」の状態で、互いに素の場合でのみ使えるという点も覚えておきましょう。 ユークリッド互除法を使って実際に「109x+35y=1」の整数解を求める方法を解説します。. 【高校数学】不定方程式とは?定義・具体例・n進数との関係性 . 不定方程式ax+by=1では、aとbが互いに素であるとき、ax+by=1 が整数解を持つという定理が成り立ちます。 互いに素とは、aとbの両方を割り切れる正の整数が1しかない、つまりaとbの最大公約数が1であるという意味です。. ユークリッドの互除法の証明と不定方程式 | 高校数学の美しい物語. 不定方程式. 整数. 更新 2021/03/07. ユークリッドの互除法(ごじょほう)とは,大きな数たちの最大公約数を素早く計算する方法です。 この記事では, ユークリッドの互除法のやり方 や ユークリッドの互除法の不定方程式への応用方法 などを解説します。 目次. ユークリッドの互除法の例. 最大公約数の記号. ユークリッドの互除法の証明. ユークリッドの互除法がなぜ嬉しいのか. 一次不定方程式への応用. まとめ. ユークリッドの互除法の例. ユークリッドの互除法では,以下の 重要な性質 を使って最大公約数の計算を行います。 重要な性質. 割り算の等式: a=bq+r a = bq+ r において, 「 a a と b b の最大公約数」=「 b b と r r の最大公約数」 例. 整数の性質|不定方程式の整数解を求めるときに「互いに素」を . 【整数の性質】不定方程式の整数解を求めるときに「互いに素」を利用する理由 3( x +2)-7( y +1)=0とあって,3と7が互いに素だから,なぜ x +2は7の倍数になるのかがわかりません。. 不定方程式・その1 導入から基本解法パターンまで | 高校数学の . 不定方程式 導入. x,y x, y に関する 2 2 元 1 1 次方程式 ax+by = 1 a x + b y = 1 の整数解を求めましょう。. ただし、 a,b a, b ともに整数であるとします。. 具体例で考えましょう。. a = 2,b = 7 a = 2, b = 7 のとき. 2x+ 7y = 1 2 x + 7 y = 1. 未知数が x,y x, y と 2 2 つあるの . ax+by=c型1次不定方程式(合同式を利用する裏技) - 受験の月. ユークリッドの互除法を必要としない場合の解法。 examist.jp. また、前項の正攻法を習得済みであることも前提とする。 ax+by=c型1次不定方程式(ユークリッドの互除法の利用) 定期試験・大学入試に特化した解説。 係数が大きくて特殊解を見つけにくい場合、最大公約数をユークリッドの互除法で求める過程を逆に辿る。 examist.jp. 検索用コード. 1次不定方程式$ax+by=c$を解くには, まず解を1組見つける必要があるのであった. 釣っ た 魚 を その 場 で 食べる 関西
キョエ ちゃん 声 変わっ た前項で述べたように, ユークリッドの互除法を利用すると確実に見つけることができる. しかし, 処理や記述が多くなりがちで, 時間制限のある試験では, できれば避けたい. そこで合同式を利用する (裏技).. ax+by=c型1次不定方程式(ユークリッドの互除法の利用 . 
2023.12.15. 本項の内容は、以下の基本的な型を習得済みであることを前提とする。 基本的なax+by=c型の不定方程式(aX=bY型の不定方程式) 定期試験・大学入試に特化した解説。 高校数学最重要問題の1つ。 ユークリッドの互除法を必要としない場合の解法。 examist.jp. 本項の重要さが一目瞭然でわかるツイート^^. 不定方程式とは?問題の解き方を種類別にわかりやすく解説 . コスモ 調布 ヶ 丘
黒髪 に 合う カラコン(4) と (−5) は互いに素なので、((x + 1)) は (−5) の倍数、((y − 1)) は (4) の倍数でないといけませんね。 これを、任意の整数を用いて表現しましょう((k, m) など、なんでもOK)。. 不定方程式の解き方4パターンとは?【方程式の整数解の問題9 . 本記事では、一次不定方程式の特殊解の見つけ方から、ユークリッドの互除法を用いる問題、さらに一次不定方程式の応用問題3選まで、わかりやすく解説します。 「一次不定方程式マスター」になりたい方必見です。 数学太郎. 一次不定方程式も重要だけど、他の不定方程式の解き方も知りたいな。. 不定方程式の整数解【例題4問と解き方6パターン】 - 学びTimes. バレエ コンクール で 入賞 し やすい 曲
薬 を 飲ん でも 熱 が 下がら ない解答. x=4,y=-2 x = 4,y = −2 は解の2つである。 3times 4+5times (-2)=2 3× 4+5×(−2)= 2. これをもとの方程式を引き算すると. 3 (x-4)+5 (y+2)=0 3(x −4)+5(y +2) = 0. 3 3 と 5 5 は互いに素なので x-4=5m x−4 = 5m とおける。 このとき y+2=-3m y+ 2 = −3m となる。 よって答えは. (x,y)= (4+5m,-2-3m) (x,y) = (4+ 5m,−2− 3m) 2変数の1次不定方程式です。 詳細は →一次不定方程式ax+by=cの整数解. 割り算の余りに着目するパターン. 例題2. 一次不定方程式の解き方! 練習問題でマスターしよう|高校生 . 一般に、不定方程式では整数解が求められます。 例えば、3x=2yにおいて整数解を求めることを考えましょう。 このとき注目したいのは、 変数の前にある係数 です。 右辺には係数として2がありますから、2yは2の倍数です。 一方、左辺を見ると係数は3です。 したがって、変数xは2の倍数であるはずです。 このことを整数nを用いて数式で表現してみましょう。 x=2nとおいて、元の式に代入すると. 3・2n=2y. 6n=2y. y=3n. となり、さきほどx=2n とおきましたから、 (x, y)= (2n, 3n)が一般解です。 次に、右辺に定数項があるケースを考えましょう。 3x+2y=1の整数解を考えてみると、直感的に (x, y)= (1, -1)が浮かぶでしょう。 ここから、. 互いに素とは?意味や証明問題を簡単にわかりやすく解説 . 利用問題①「二元一次不定方程式」 利用問題②「合同式の商」 互いに素とは? 互いに素とは、 つの整数の最大公約数が であること です。 互いに素の定義. つの整数 を共に割り切る整数が と のみ、すなわち の最大公約数が であるとき、「 と は互いに素である 」という。 特に、 はすべての整数に対して互いに素となる。 整数を扱う問題では、「互いに素」という性質は非常に強い条件として使えます。 合わせて読みたい. 最大公約数とは? 意味や簡単な求め方、計算問題. 互いに素である・互いに素でない例. 例えば、次の 数 が互いに素であるかを見てみましょう。 (例) 公約数は と. → 互いに素. 公約数は と. パン こね 機 こね 丸 くん
も も も 合衆国 漫画→ 互いに素. 不定方程式とは?基礎知識と解き方を解説! - 受験のミカタ. 2.不定方程式の例:互いに素. 犬 と 泊まれる 宿 石川 県
歯 固め 歯並び に 影響不定方程式としてシンプルな形で出題されるのが、 「4x=3y (xとyは整数)を解け」 、というものです。. この形だと、左辺と右辺から互いに素を利用して、一般的な解を求めるのがシンプルで簡単でしょう。. 互いに素とは . 不定方程式・その2 右辺が1でないとき | 高校数学の無料 . 
右辺が (1) じゃないときもあるの?前ページでは、(ax+by=1) という不定方程式を見てきました。そして、(a,b) が互いに素であるときに整数解を持つことも確認しました。 ここでは、右辺が (1) にならないケースについてみておきましょう。. 素数にまつわる覚えておくべき性質まとめ | 高校数学の美しい物語. まとめ. 更新 2021/03/07. 素数について,ついでに互いに素な2つの整数について,覚えておくべきことを整理しました。 比較的レベルが高い内容になっています。 目次. 素数の基本的な性質,定理. 「互いに素」についての性質. 教養としての素数の知識. 素数の基本的な性質,定理. ・ p p が素数, m, n m,n が整数で, mn=p mn = p なら m m か n n のどちらかの絶対値が 1 1 。 これは素数の定義から当たり前の事実ですが不定方程式を解くときなどに使う基本的な性質です。 ・素数 p p と任意の自然数 a a に対して. a^pequiv apmod {p} ap ≡ a (mod p) →フェルマーの小定理の証明と例題. 一次不定方程式の解き方とは?【応用問題3選もわかりやすく . ちなみに不定方程式とは、$ax+by=c$( $a$,$b$,$c$ は自然数)のように、解が有限個に定まらない方程式のことを指します。 数学太郎. 一次不定方程式の解き方がわからないです…。 こういった悩みを抱えている方は多いでしょう。 よって本記事では、一次不定方程式の解き方のポイントから、一次不定方程式の応用問題 $3$ 選まで. 東北大学理学部数学科卒業. 教員採用試験に1発合格 → 高校教諭経験アリ. の僕がわかりやすく解説します。. 【大学受験】数学の不定方程式とは?特殊解、合同式について . 例えば、ax + by = c の形の不定方程式において、aとbが互いに素である場合、この不定方程式は特殊解を持ちます。 この場合、特殊解は、x = c(mod b)かつy = (c - ax) / b という形式で表すことができます。 この特殊解を求めることによって、不定方程式の解を求めることができます。 また、不定方程式には、特殊解が存在しない場合もあります。 この場合、不定方程式の解を求めるためには、一般解を求める必要があります。 合同式と不定方程式との関係は? 合同式と不定方程式は、数学的に密接に関係しています。 合同式は、2つの整数の差が、ある整数nの倍数である場合に成立する式のことを指します。 例えば、a ≡ b (mod n)は、aとbの差がnの倍数である場合に成立する式です。. 【高校数学A】「ax+by=1の整数解」 | 映像授業のTry IT . 不定方程式ax+by=1の一般解を求めるときには、まず 代入 によって 解を1組だけ見つける んだ。 例えば、3x+2y=1を満たす整数解1組だけなら、 (x,y)= (1,-1)がすぐ見つかるね。 連立方程式のように並べてひく! POINT. 〔手順1〕によって整数解1組が見つかったら、 連立方程式のように並べて引いてみよう。 3x+2y=1……①. 3×1+2× (-1)=1……②. ①-②をすると, 3 (x-1)+2 (y+1)=0. ⇔ 3 (x-1)=-2 (y+1) この形なら、 互いに素 な性質を利用することで、一般解 (x,y)が求められそうだね! どうかな? 具体的な解法は次のページで確認しよう。 この授業の先生. 今川 和哉 先生. 互いに素 - Wikipedia. 互いに素とは、数学の複数分野で使われる用語である。 集合論 互いに素 (集合論) → 素集合 整数論 互いに素 (整数論) 代数学 2つの多項式が「互いに素である」とは、両者をともに割り切るような多項式が存在しないこと、つまり、それぞれの多項式の因数分解で共通の因数が現れないことで . 46xー35y=3という不定方程式をユークリッド互除法を使ってもとめ . 次に、不定方程式46X - 35Y = 3を解きます。最大公約数が1であるため、この方程式の解は存在します。 方程式を変形して、46X = 35Y + 3とします。これを満たす整数解を見つけるために、XとYに適当な値を代入します。例えば、X=1, Y. 不定方程式の解き方がたった15分で理解できて問題を解ける【数学ia】 | Himokuri. 無数に解が存在する一次不定方程式。では、一次不定方程式を解くとはどういうことなのでしょうか。 答えは、 すべての解を表せる式を求める ことです。 少しむずかしいですね。次の項で実際に問題を解きながら、理解を深めていきましょう。 一次不定 . 【1次不定方程式】整数解(特殊解)を「合同式(mod)」で一瞬で見つける裏ワザ【練習問題つき】│楽スタ!. この問題がスラスラ解ければ、大学入試で 1次不定方程式 の問題が出ても安心です! 【まとめ】1次不定方程式の整数解(特殊解)を「合同式(mod)」で見つける裏ワザ. 最後に、 1次不定方程式の整数解(特殊解)の見つけ方( 裏ワザ ) をまとめておきます。. 1次不定方程式 | おいしい数学. 1次不定方程式と解法. x x , y y の1次方程式 ( a a , b b , c c は整数. a ≠ 0 a ≠ 0 , b ≠ 0 b ≠ 0 ) ax+by = c a x + b y = c. は未知の文字 x x , y y に対して式が1つしかないので解が1つに定まらず,このような方程式を 不定方程式 といいます.不定方程式を成立さ . 中国剰余定理と法が互いに素でない場合への拡張 | 高校数学の美しい物語. この記事はその発展です。以下では,二元の場合の結果と考え方を用いるので先に二元の場合をしっかり理解しておいてください! このページでは, 合同式が3本以上ある場合; n i n_i n i たちが互いに素でない場合; を考えます。. 1次不定方程式を「中学生でもわかる」ように基礎から教えてほしいです。よろしくお願 | アンサーズ. これが原因なのです。. 一般に、 ax+by=1 ax +by = 1という不定方程式の a a, b bが互いに素でないときには、整数解をもちません。. 対偶という考え方を用いると簡単に証明もできます。. また、解が簡単に見つからないときには「ユークリッドの互除法」という . ユークリッドの互除法と一次不定方程式 - 高校数学.net. ユークリッドの互除法と互いに素. ax + by = 1 の形の一次不定方程式を解くとき、 x, y が整数なら a と b が互いに素じゃないといけないんだ。. 大切なことだから覚えておこう。. 例えば a = 2, b = 4 だと 2x + 4y = 1 になって左辺は 2(x + 2y) って a = 2 と b = 4 の最大 . 2元1次方程式の整数解 | わかる数学. なので、( 29 と 17 ) は互いに素なのですが、 その ( 29から17 ) を引いた ( 12と17 ) は互いに素になる. のかという疑問です。 つまり上の話で行けば、( 29と17 )の世界では単位が(1)(:最大公約数) になるのかという事です。 下記の補足証明が必要です。. 互いに素な自然数とは?【応用例7選もわかりやすく解説します】. 目次. 互いに素な自然数とは?. 【「最大公約数が1」という意味です】. 「互いに素」であるとは、共通な素因数を持たないことと定義しました。. これを、今までで習った言葉に置き換えると…. 最大公約数が $1$ である. と表すこともできます。. 式にする . 互いに素な整数に成り立つ重要な定理 | 高校数学マスター. 互いに素な整数に成り立つ定理を今回は証明します。この定理は、整数に関する基本的な定理で、様々な定理の証明のポイントとして使われますので、教科書では証明抜きで紹介されていますが、きちんと証明まで理解しておくと良いと思います。. 1次不定方程式の解き方4通り | 数学の庭. 1次不定方程式の解き方4通り. 整数 不定方程式. 1次不定方程式 ax+by=1 の整数解を求める方法を4通り紹介します。. ax+by=1 の解き方を知っていればax+by=c も解けます。. →1次不定方程式を解くときに知っておきたい3つの基本知識. 当記事では、次の例題を4通りの . 高校数学: 不定方程式の解. ですから,お題のように c = 1 の場合には,この不定方程式が整数解をもつためには a と b が互いに素でなくてはならないのです. 解き方は,方程式を満たす整数解を1つだけ見つければ解決します. 線 対称 な 図形 書き方
白髪染め 長持ち させる に は(1) を満たす x と y は直ぐに見つかりますね・・・例えば (x, y . ユークリッド互除法と2元1次不定方程式!例題で分かりやすく理解|高校生向け受験応援メディア「受験のミカタ」. 今回は数学Aの範囲でもあるユークリッドの互除法について例題を使いながら解説します!ユークリッド互除法は2元1次不定方程式の解を求める時にも役に立ちます。ユークリッド互除法の基礎から証明、例題を使ってわかりやすく説明していきます。. 互いに素とその意味について|思考力を鍛える数学 - 思考力を鍛える数学. 特に,$1$ と全ての数は互いに素です. 互いに素というのは言い換えれば,共通の素因数を持たないということです.たとえば,$8$ の素因数は $2$ で,$21$ の素因数は $3,7$ です.したがって,$8$ と $21$ は共通の素因数を持っていないので,互いに素です.. 【高校数学a】互いに素な自然数の性質とその証明 | 受験の月. 高校数学総覧. 高校数学A 整数. 互いに素な自然数の性質とその証明. 互いに素な自然数の性質とその証明. 2021.04.19. 検索用コード. 代々木 アニメーション 学院 面接
チョッパー ヒトヒト の 実 モデル
連続する2つの自然数が互いに素であることを示せ. (2) 連続する2つの正の奇数が互いに素であることを示せ. 互いに素な自然数 . 3文字の一次不定方程式の解き方を合同式でパターン化しておきたいなら | 数学のコツ壺 / 風いま数学協室. (i-a) 互いに素でない係数の組が2つ以上のときは、一般解が2つ求まるので元の式に代入して残りの一般解を求める。 (1-b) 互いに素でない係数の組が1つ以下のときは、一般解が1つ求まるので元の式に代入する。すると2元一次不定方程式に帰着される。. 一次不定方程式 - 計算が簡単にできる電卓サイト. ひとつの方程式しかないのに文字が2つありますね。これだと解が(x,y)=(2,-1)や(x,y)=(5,-3)など何通りもあります。このように 解がひとつに定まらない一次方程式のことを一次不定方程式 と言います。. ではこのような解が定まらない一次不定方程式をどうやって解くのかというと一般解という形で . 
【整数】合同式(mod)は習わない?知ってると便利な使い方を紹介 | 粗茶ですが…. ここで右辺は13の倍数である。等式が成り立つためには左辺も13の倍数でなくてはならない。 7と13は互いに素であり,7は13の倍数ではないので, x-2 が13の倍数である。 よって, x-2=13k ( k は整数)とおくことができ,上の式に代入することで, y-1=7k も . 互いに素とは? 背理法を使った証明の例題・合同式との関係も合わせて解説|高校生向け受験応援メディア「受験のミカタ」. 3. 合同式と互いに素. 合同式 は、一般的な高校の教科書では発展型として紹介されるくらいで、あまり詳しくは習いません。 センタ-試験にも出題されることはありませんが、実は難関大学の入試では合同式を知らないと解きづらい問題が出題されることがあります。. 方程式の整数解 -不定方程式-【昭和女子大・立命館大】 | 大学入試数学の考え方と解法. 方程式の整数解に関する様々な問題が,大学入試で出題されますが,今回はその中でも特に出題頻度が高いものを扱います。様々な問題を解くことで,解法を知って,解ける問題を増やしていきましょう。不定方程式の基本問題ヒロまずは簡単な問題から不定方程式の. 【一次不定方程式】なぜユークリッドの互除法で特殊解が求められるのか?分かりやすく解説 - Manami-Math. これには 23と16が 互いに素 (公約数が1のみ)であることが大事なのです。 そして、次の命題が成り立つことを意識する必要があります。 (a-bq=r) で (a, b) が互いに素であれば、(b, r) も互いに素になる。 特に上式を割り算とみなして言葉で言えば、. ユークリッドの互除法による1次不定方程式の特殊解の出し方. 155 155 が x x 個と, 42 42 が y y 個足して 1 1 になるという問題で (当然今回は x x か y y どちらか負), ユークリッドの互除法 を使って解きます.. 解答と解説. ユークリッドの互除法を用いて, 155 155 と 42 42 の最大公約数が1 (互いに素)であることを計算して . 
PDF 12 月 第3回 ユークリッドの互除法と 次不定方程式 35. 10 テーマ 番号 整数の性質 35 12 月 授 業 第3回 ユークリッドの互除法と1 次不定方程式 1 次不定方程式の整数解を求めるには, 1 組の整数解 (,xy 00 ) を見つけて, ab()xx-+ 0]gyy-= 0 0 の形にする 1 組の整数解を見つけるのが難しいときは,ユークリッドの互除法の逆をたど. 1次不定方程式 | 教えて数学理科. k は任意の整数なので、解が無数にあることが分かります。. この例 2x = 5y のような、1次式 ( x, y どちらも1次)で表された方程式を1次不定方程式といいます。. 文字2つに式1つなので、一般的には解が無数にあります (不定)。. 1次不定方程式 ax + by = c a ≠ 0, b . 春の 野草 イネ 科
個展 の 案内 状【整数問題】不定方程式を瞬時に解く技術 | 初心者医学生の雑記ブログ. かつ2と31は互いに素であるので、割り算の合同式を使うことができるので両辺を2で割って、 (yequiv16(mod31))となりました。 この式の意味は(y)を31で割ったあまりは16だよっていうのを表しています。. ユークリッドの互除法とは?証明ややり方をわかりやすく解説! | 受験辞典. 互いに素な (2) 数の最大公約数が (1) であることに着目すると、(a, b) に対して余り (bf{1}) となるまでユークリッドの互除法を使うことで特殊解を求められます。 問題を通して、使い方を見てみましょう。. PDF 6章 合同式を解く - 学校法人学習院. 24 第6章 合同式を解く n1 nr 0 (mod p) をみたす素数p が存在する.とくにm2 mr = n1 0 (mod p) より,mj 0 (mod p) をみたす2 j r がとれるが,これはmj;nj が互いに 素であることに矛盾する.よってgcd(n1;:::;nr) = 1 が示され,定理3.4 よりn1t1 + +nrtr = 1 をみたすt1;:::;tr 2 Z が存在する.このとき,ni の定義から,1 i . 【一次不定方程式】当てはまる整数解(特殊解)の求め方 | すうがくブログ【式変形ch/教採数学ch】. 【一次不定方程式】当てはまる整数解(特殊解)の求め方. 今回の内容(プラスα)の動画版→一次不定方程式、3つの解法 一次不定方程式の特殊解を求める方法を2通り紹介します。2019年のセンター試験で出題されたものを利用することにしましょう。. 合同式(mod)とは?性質の証明や計算問題の解き方 | 受験辞典. この記事では、「合同式 ((bmod))」についてわかりやすく解説していきます。 合同式の性質や解き方、不定方程式との関係なども説明していきますので、ぜひこの記事を通してマスターしてくださいね。 目次合同式とは . 互いに素の関係:最大公約数・最小公倍数と証明問題 | Hatsudy:総合学習サイト. 互いに素というのは、要は共通する素因数をもたないことを意味します。このとき、互いに素である場合は3つの性質があります。互いに素である関係に加えて、最大公約数と最小公倍数を利用することによって新たな関係式を作れるのです。. PDF 2元1次不定方程式特殊解の簡便法による求め方. これを用いると互いの素である2数をx y, の係数とする二元一次不定方程式は,互除法により特殊解を求め ることが可能になる. 互除法による二元一次不定方程式の特殊解の求め方 不定方程式 501 217 1x y+ =の特殊解を求めてみよう.. 合同式(mod)を応用して京大入試問題を解こう【不定方程式の問題も解説】 | 遊ぶ数学. 合同式は、除法のみ「互いに素」に注意しなくてはいけないということですね。 互いに素については「 互いに素な自然数とは? 【応用例7選もわかりやすく解説します】 」の記事で詳しく解説してます。. タニタ 食堂 せんべい どこに 売っ てる
礼服 どこで 買う メンズ合同式(mod)の問題と使い方を超わかりやすく説明してみた | 理系ラボ. このように、 「割る数」と「法」が互いに素でないと、合同式の除法の性質は使えません 。 3. 合同式の使い方. それでは、合同式を使った例題を実際にみてみましょう。 3.1 【例題1】合同式の方程式. 一次不定方程式の解の存在 - さくらのレンタルサーバ. 一次不定方程式の解の存在. のとき解をもつことが示せれば,例えば なら を考えればこの場合も整数解があることがわかる.. よって と は である互いに素な整数とする.. この定理には三通りの証明法がある.それを実行し比較検討しよう.. 拡張ユークリッドの互除法 〜 一次不定方程式 ax + by = c の解き方 〜 #競技プログラミング - Qiita. NTT データ数理システムでアルゴリズムの探求をしている大槻 (通称、けんちょん) です。好きなアルゴリズムは二部マッチングです。 今回は、歴史の記録に残る最古のアルゴリズムの 1 つとして知られるユークリッドの互除法について書きます。. 足 に 物 を 落とし た
ユークリッドの互除法は、最大公約数を求め . 【高校数学A】「「互いに素」とは?」 | 映像授業のTry IT (トライイット). Try IT(トライイット)の「互いに素」とは?の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の . 【基本】不定一次方程式の整数解 ax+by=0の場合 | なかけんの数学ノート. なので、 x は「91 × ある整数」と書ける・・・ わけじゃない んですね。 係数が互いに素(最大公約数が1)なら正しいのですが、今の場合互いに素ではありません。52も91も、13の倍数なんですね。なので、両辺を13で割って[ 4x=-7y ]と変形します。. 【整数】1次不定方程式〜合同式(mod)利用〜【裏技】. 1次方程式についての基本は、以下の記事で解説しています。. 【整数】不定方程式 〜定期テストプラス10点〜【解き方】. 今回は、不定方程式の解き方の基本を解説します。. 不定方程式ってなんかごちゃごちゃしていてよく分からないんだよな、、、。. と . 【ユークリッドの互除法は無理という人へ】不定方程式は合同式を試してみて | 数学のコツ壺 / 風いま数学協室. 7で割ったときの余りが1になるのは、1以外に7つごとに無数に存在します。 4x≡1≡8≡15 (mod 7) などとなります。小さい方にずれていくと. 4x≡1≡-6≡-13 (mod 7) などとなります。 合同式はいつでも割れるわけではないですが、mod と互いに素な数は割り算できます。. 【問題】不定方程式 | 数学好きの大学受験数学. 数学. コピー. 2021.06.26. 不定方程式は、方程式の数よりも未知数の数が多い方程式のことです。. たとえば、 x, y の文字が2つあった場合、2つの方程式があれば、これを連立方程式と呼び、 x, y を求めることができます。. 一方、式が1つしかない場合には不定 . ユークリッドの互除法とは? 計算例、なぜうまくいくか | 趣味の大学数学. よって、(mathrm{gcd}(201,80)=1)で、互いに素であることがわかりました。結局余りが1になるまで割り切れず、こういうケースは公約数が1しかないのです。2つの整数が互いに素であることの判定法としても使えますね。. 入試数学コンテスト第3回第5問解答解説 | 高校数学の美しい物語. 2021 2021 2021 と互いに素である整数は, 43 43 43 でも 47 47 47 割り切れない整数になります。 そのため 2021 2021 2021 以下の整数で 43 43 43 か 47 47 47 で割り切れる整数の集合を持ってきて,これの補集合を考えればよいのです。.





